Published on February 6, 2023
Reading Time: 6 min
UCAT Decision Making: Syllogisms
What Is a UCAT Decision Making Syllogism?
UCAT syllogisms are a method of logical reasoning used to derive a conclusion from two or more premises. Although the statements and conclusions may not make sense in reality, they’ll logically follow from the information provided. You will find syllogisms in the Decision Making section of the UCAT.
Here’s an example UCAT syllogism:
Based on the statements below, is the conclusion true or false?
Statement 1: All dogs are animals.
Statement 2: All animals have four legs.
Conclusion: All dogs have four legs.
The conclusion is true. We can see from this statement that the conclusion logically follows. If all dogs are animals, and all animals have four legs, we can logically conclude that all dogs have four legs. We have used statement 1 and statement 2 to come to a logical conclusion. This is a simple example of a UCAT syllogism question where you must use the conditions given in a question to arrive at a conclusion.
Sometimes the information provided may not be logical in real life. This can be demonstrated through the following example:
All dogs are animals.
All animals are human.
Thus, all dogs are human.
These statements are clearly untrue in real life. However, from the information provided, the conclusion logically follows. It’s essential that you use the information provided to derive conclusions when answering UCAT syllogisms rather than any outside knowledge.
How Many Syllogisms Are in the UCAT?
The Decision Making subtest of the UCAT will contain 9 syllogisms. See more below to learn the format for UCAT syllogisms questions as well an example UCAT syllogism question to practice your skills!
How Are UCAT Syllogisms Marked?
UCAT syllogisms questions will contain information followed by a series of conclusions. You must decide whether or not each conclusion can be drawn from the information provided. Questions are in a drag-and-drop format, where you must drag the “Yes” and “No” buttons, dropping them next to the correct conclusion.
Going through UCAT practice questions can help to significantly improve your UCAT score and make you accustomed to syllogisms. You can find UCAT practice papers and a variety of UCAT syllogism practice questions in our our specialist UCAT book which is fully updated for 2023, ‘Master the UCAT By the Top 1%’.
UCAT Decision Making Syllogisms Question Format
A typical UCAT syllogism question would appear as such:
All scholars at the conference who study Biology also study Philosophy. All the scholars in the conference were students at the ABC university. None of the scholars studied Mathematics, and a few of them liked environmental studies. All the scholars present had a strong inclination to believe that global warming is impacting the ecyology adversely.
Place “Yes” if the conclusion does follow. Place “No” if the conclusion does not follow.

Note: The above represents the official UCAT version of syllogism questions, whereby you must drag and drop the “Yes” and “No” from the right side into the dark grey boxes next to each conclusion. You can find more similar questions in UCAT past papers (link to the official UCAT website). The questions in this post will be in plain text format for ease.
You must understand the following definitions to answer these questions:
- Yes: From the information given in the text, this statement logically follows. The answer is only “Yes” if you are certain that the given conclusion can be made.
- No: From the information given in the text, this statement does not logically follow. There is not a 100% logical conclusion that can be made. Even with a small amount of doubt, the answer will be “No”.
Your analysis of the information provided in each question must be very clear in order to answer the question with certainty. Let us try the following syllogism example. Practice summarising the information as you read the example question.
UCAT Decision Making Syllogisms Question
All those who are thirsty are hungry. Motorcyclists are always hungry, but they are not always thirsty. All those who are intelligent are not always thirsty, but they are always hungry.
Place “Yes” if the conclusion does follow. Place “No” if the conclusion does not follow.
- All those who are hungry are intelligent.
- Someone who is hungry will not be a thirsty motorcyclist.
- An intelligent person cannot be hungry.
- Some intelligent people will not be motorcyclists.
- More intelligent people are hungry than thirsty.
UCAT Decision Making Syllogisms Answer
We can work this out by quickly writing the information in an easy-to-understand model. Let us represent Thirsty with “T”, Hungry with “H”, Motorcyclists with “M” and Intelligent with “I”. Going through the written passage above, we can deduce that:
All T → H
All M → H
Some M → T (they are not all thirsty, so some must be thirsty)
Some I → T
All I → H
Now, let us assess each of the options.
- All those who are hungry are intelligent
We know that all I → H, but this does not mean all H → I. Thus, this statement does not logically follow, and the answer is no. It is important to understand that a sentence of logic usually only flows in one direction, so do not mix up the order as the logic does not flow both ways.
For example: “All dentists learn how to drill”. This can be broken up into:
A= Dentists
B= Learning how to drill
We can therefore say A → B
However, we cannot say that everyone who learns how to drill is a dentist. This would not follow from the above statement as logic flows in one direction.
- Someone who is hungry will not be a thirsty motorcyclist.
We know that:
Some M → T
All M → H
If some motorcyclists are thirsty, and all motorcyclists are hungry, we can logically conclude that a thirsty motorcyclist will be hungry.
- An intelligent person cannot be hungry.
No, because the information we are given tells us that all intelligent people are hungry.
All I → H
- Some intelligent people will not be motorcyclists.
No, as there is no logical relationship we can conclude with certainty about intelligent people and motorcyclists. Remember that certainty of relationships only goes in one direction.
- More intelligent people are hungry than thirsty.
Yes, as All I → H whereas only some I →T. We can logically conclude that there are more intelligent people who are hungry than thirsty.
Finding this useful? It’s an excerpt from our popular UCAT content, created by top 1% scoring candidates! Check out the best UCAT resources, such as our 2-day live UCAT course, online UCAT course (175 lessons), UCAT book, and one-to-one UCAT tutoring for more UCAT support.
Venn Diagrams For UCAT Syllogisms
Around a third of UCAT syllogism questions can be solved using Venn diagrams. Learning this technique can really help to improve your average UCAT score. There are seven Venn diagrams that we have named the “Seven HeaVenns”. Going through these Seven HeaVenns, you will learn to appreciate how Venn diagrams can be used to clarify the relationships between different objects in a syllogism. Thus, you will be able to quickly and accurately draw logical conclusions from the given text.
1st HeaVenn: No X are Y
We can express this visually by using the following Venn diagram. The orange outlined shape is X and the black outlined shape is Y.
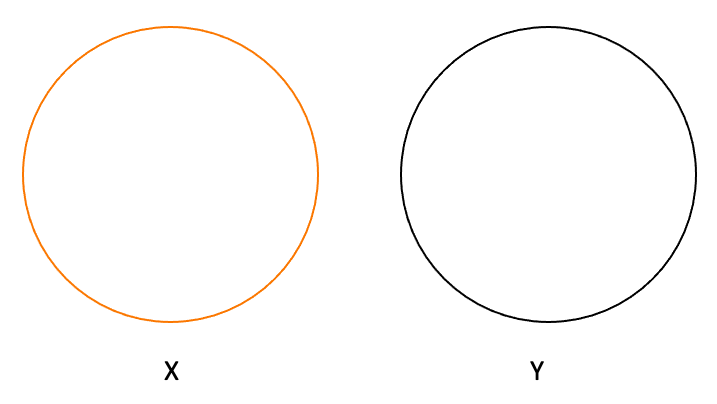
As per the above image, it is evident that No X are Y. We can also deduce from the statement that No Y are X. This is reinforced by the image.
Let us now replace “X” and “Y” with nouns.
Rather than “No X are Y”, if the statement was “No shoes are boots,” we could also logically conclude from the statement, with the help of the Venn diagram, that no boots are shoes.
2nd HeaVenn: Some X are Y
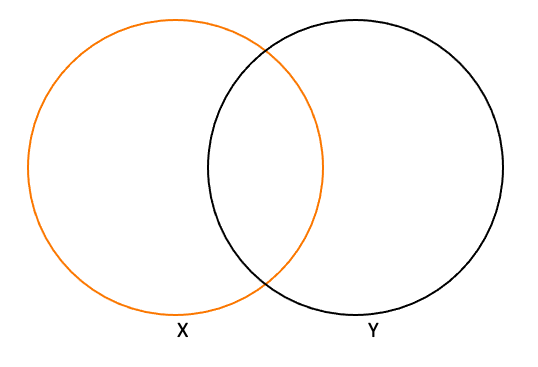
The statement above has been manipulated into a Venn diagram. This now makes it easier for us to make further logical conclusions. We already know that “Some X are Y”. We can now say that the following conclusions also logically follow:
- Some Y are X
- Some X are not Y
- Some Y are not X
If we replaced X and Y with nouns and the statement was “some lions are mammals”, we could draw the following Venn diagram:

We can easily deduce that some lions are mammals, some mammals are lions, some lions are not mammals and some mammals are not lions. All of the statements mentioned are logical conclusions that can be made. Although we know from our outside knowledge that all lions are in fact mammals, this statement does not logically follow from the information provided. You must remember not use any outside knowledge when interpreting UCAT syllogisms.
You can find details of the other HeaVenns in our 500-page UCAT book.
We hope this article was useful for your UCAT preparation! It’s an excerpt from our popular UCAT resources, created by top 1% scoring candidates!













