Published on July 6, 2023
Reading Time: 13 min
UCAT Decision Making Tips, Questions & Strategies
Decision Making is the second section of the UCAT test which assesses your ability to deduce information from complex sources of data. It tests how well you can interpret and decipher details, and extrapolate inferred information to derive conclusions.
The Decision Making section comes after the Verbal Reasoning section and before the Quantitative Reasoning section. The data within the questions is given in the form of passages, graphs, charts, visual diagrams, and text. Some questions have concepts taken from Verbal Reasoning and Quantitative Reasoning. It’s worth revising some critical thinking material to prepare for this section.
In this article, you’ll learn how to answer questions involving Venn diagrams, syllogisms, drawing conclusions, shape equations, and more! The best time-saving strategies are explained in detail to help you understand each question.
UCAT Decision Making Score
In 2024, the Decision Making UCAT subtest had the second lowest overall average score of 620. From 2018-2022, the Decision Making subtest average scores have ranged between 610-625, making it the second lowest scoring section next to Verbal Reasoning. Keep reading our blog post for the best tips and tricks to acing UCAT Decision Making, as well as sample questions and explanations!
What’s a Good UCAT Decision Making Score?
A “good” Decision Making score would be one that’s above the average for your testing cycle. The Decision Making (DM) section is scored between 300 and 900, just like the other cognitive subtests in the UCAT. Over the past few years, the average score for DM has been around 630–660.
| Year | Decision Making Score Average |
| 2022 | 616 |
| 2023 | 623 |
| 2024 | 620 |
A score of 700 or above in Decision Making is considered excellent, but even achieving a score above the average (typically around 650) is still regarded as doing quite well. Also, universities will usually focus on your overall UCAT score rather than looking at individual subsections.
Our free resource has the most up-to-date UCAT scores needed for medicine for each university in 2025. Check out ‘Master the UCAT by the Top 1%‘, our #1 Amazon Bestselling UCAT book (second edition updated for the 2025 UCAT syllabus) to learn all the tips and tricks necessary for improving your score and achieving 800+ on Decision Making!
UCAT Tutoring by Top 10% Scorers
Skyrocket your UCAT score with one-on-one mentoring with an expert UCAT tutor. We focus on your weakest areas and deliver personalised preparation to help you reach your highest potential.
How is UCAT Decision Making Scored?
Understanding UCAT Decision Making scoring system is crucial for maximizing your performance. The scoring breakdown is as follows:
- Single-answer questions: 1 mark each.
- Multiple-statement questions: 2 marks for a fully correct response.
- Partially correct responses: Awarded 1 mark instead of 2.
This system is used specifically in multiple-statement questions. It ensures that you are recognized for partial accuracy. This means you can earn marks even if only some of your responses are correct. These questions test your ability to evaluate several independent statements based on a scenario. For example, you may be asked to decide which of the statements are true or false (you’ll be provided 4 to 5 statements for evaluation). You can learn more about the different Decision Making timing and question types below.
UCAT Decision Making Time
As updated for the 2025 UCAT, there are 35 questions in the UCAT Decision Making subtest with 37 minutes given for this section, giving you approximately 63 seconds per question.
Decision Making Question Types
The various types of Decision Making questions are listed in the table below. Some questions will take longer to complete, while some should take less time. You can refer back to this table once you familiarise yourself with the types of questions. A large portion of questions will require use of your whiteboard, and some will require you to use the on-screen calculator.
| Category | Question Types | Time Needed | Number of Questions |
| Statistical and Figural Reasoning | – Venn Diagrams – Probabilistic Reasoning | – Probabilistic Reasoning – 40-60 seconds | Approximately 10-11 Questions |
| Deductive Reasoning | – Syllogisms – Logical Puzzles – Shape Equations | – 60-80 seconds – 20-30 seconds for shape equations | Approximately 11-12 Questions |
| Evaluating Arguments | – Justifying Assumptions – Drawing Conclusions | – 20-40 seconds | Approximately 11-12 Questions |
There are two formats of questions in Decision Making:
- Multiple Choice Questions: You are given a choice of 4 possible answers where you must select one. Each question is worth a single mark.
- 5 Statement Questions: Each question has 5 statements. You must assign either “Yes” or “No” to each statement.
- 5 correct = 2 marks
- 4 correct = 1 mark
- < 3 correct = 0 marks
See our example questions below to give you an idea of the general strategies used in UCAT Decision Making. We dive deeper into Decision Making strategies in our UCAT resources by top 1% scorers, such as our 2-day live UCAT course, our 154-lesson online UCAT course (bite-sized video lessons), best-selling UCAT book (updated for 2025), and one-to-one UCAT tutoring.
UCAT Decision Making Probabilistic Reasoning Example
- To work out the probability of an event and another event, multiply each individual probability.
- To work out the probability of an event or another event, add the individual probabilities.
Example:
Natalia tosses an unbiased 2-sided coin.
- What is the probability that it lands on heads?
- If she tosses it twice, what is the probability that it will land on heads both times?
- If she tosses it twice, what is the probability of landing on both heads and tails, in any order?
Strategy:
The tree diagram shows the probability of landing on heads of tails in the first and second outcome:
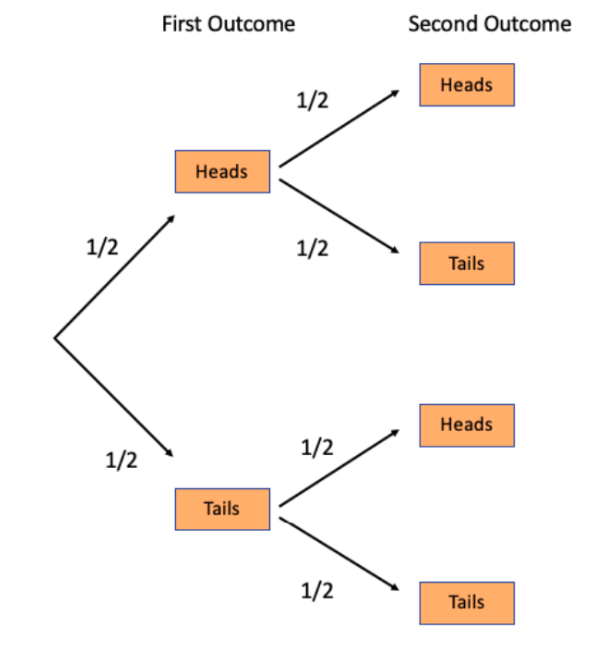
- 1. The probability that it lands on heads the first time is ½.
- 2. The first outcome must be heads and the second outcome must be heads. The two probabilities you must consider are as follows:
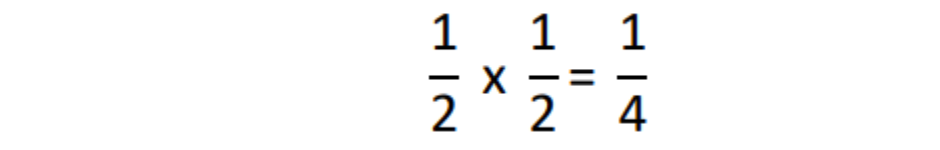
- 3. The probability of landing on heads first, then tails, can be calculated by multiplying the individual probabilities of both outcomes, as follows:
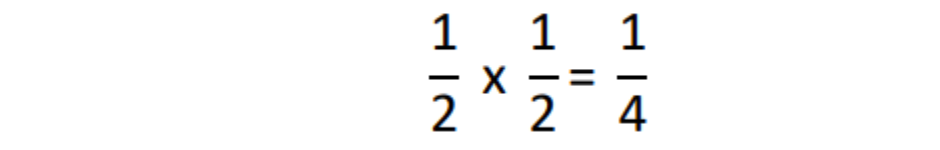
- The same can be done to calculate the probability of landing on tails first, then heads:
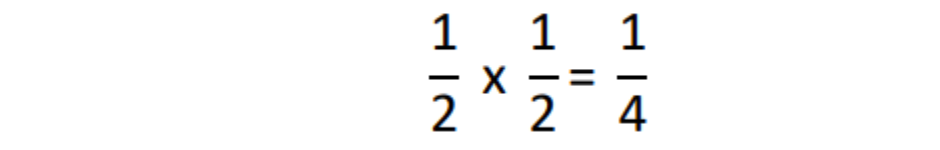
- Because there are two ways that this combination of outcomes can occur, the two individual probabilities for each combination need to be added up. Therefore, the probability of landing on heads and tails, in any order (i.e. the first combination or the second combination) is:
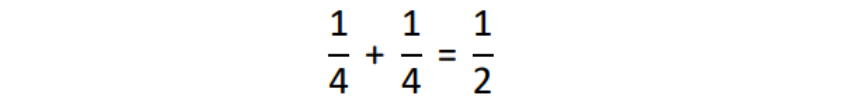

UCAT Crash Course
Maximize your UCAT score with our Intensive 2-day live course! Designed by top 1% scorers, it focuses on effective strategies and the best preparation to help you achieve your desired score.
UCAT Decision Making Shape Equations Example
Each Shape Equations question consists of four rows. Each row is an equation made of shapes. The final row has a missing shape, which you will need to decipher. This form of maths isn’t commonly practiced, so despite the equations being generally simple, they can be challenging to understand. Your whiteboard or scratchpad will be essential here. Many students like to replace the shapes with letters and solve each question algebraically, while others prefer to work with shapes. It typically takes far less time to solve equations using letters, but you can use whichever method you find easiest.
Example:

The correct answer is D. Below we will demonstrate a solution using shapes, but feel free to try this equation out algebraically as well. Remember, the first three rows are equations 1, 2, and 3 respectively, while the final row is equation 4.
Strategy:
Start with the equation that has a missing variable – equation 4. There are four different shapes, so we must try to reduce the number of shapes in order to solve the equation. If any equations from 1-3 can easily replace any of the shapes in equation 4, they should be substituted now.
- Equation 3 is simple: 1 star = 2 hearts. Substitute the star in equation 4 for 2 hearts. This will reduce the number of shapes in equation 4 from four to three.
- You can now go back to equations 1-3 to find anything else that can be substituted into equation 4. The triangle in equation 2 is equal to 1 circle and 1 heart. We can remove the triangle in equation 4 by substituting it for a circle and a heart. The goal is to reduce the number of shapes in the equation, and by replacing the triangle for a circle and heart, the number of shapes in equation 4 will be reduced from three to two.
- You can now rearrange the equation:
- 1 circle + 3 hearts = 1 circle + 1 heart + ?
- A circle on each side of the equals sign cancels out, and a heart on the right side can be subtracted on the left side to give two hearts on the left. This gives the following:
- 2 hearts = ?
- We know from equation 3 that 1 star = 2 hearts. Therefore, 2 hearts = 1 star. The missing shape is a star.
UCAT Decision Making Evaluating Arguments Example
An argument is a set of reasons that address a problem or an idea, either given in support of or against it. It’s made up of premise(s) and a conclusion (Yes/No), with the premise(s) acting as evidence for the conclusion.
| Factors That Strengthen an Argument | Factors That Weaken an Argument |
| The premises are based on facts/research/studies | The premises are based on opinion or subjectivity |
| The premises are directly linked to the subject of the argument | There is no clear link between the premise and the subject of the argument |
| The conclusion logically follows from the premises | The premises do not cover all of the points of the argument |
| No assumptions are made | Assumptions re made |
| No external knowledge is used | External knowledge is used |
- Understand the subject matter and identify key points. What exactly is being asked? Is the idea universal or does it refer to a specific group?
- Read the arguments (all of the answer options). There are likely to be options that have the correct conclusion (Yes/No) but have illogical or irrelevant reasoning. You cannot choose a conclusion (Yes/No) without reading the full argument, as the correct conclusion must be paired with the correct premises to support it.
- Eliminate any arguments that are weak due to assumptions, bias, irrelevance, or subjectivity.
- Evaluate the remaining arguments, separating them into premises and conclusions. Identify whether the premises specifically address each of the key points in the idea. Eliminate any argument that misses out a key point.
- Select the strongest argument. This should be relevant to the topic, evidence-based, and address all of the key points in the idea. You may not find the best argument to support or reject the idea, but it should be the best out of all of the options presented.
Example:
Should the legal driving age be reduced to 15 to overcome the issue of illegal driving?
Select the strongest argument from the statements below.
A. Yes, if younger people can drive, they will be happier citizens and abide by the laws.
B. Yes, by reducing the driving age you will reduce the number of young people smoking cannabis on the street.
C. No, because 15-year-olds are not mature enough to drive, so they may cause more care accidents.
D. No, because studies have shown that there is no association between age and likelihood of illegal driving.
The correct answer is D.
Strategy:
A. This is a subjective statement that is irrelevant as it isn’t directly addressing the subject matter. Although “abiding by the law” can refer to the avoidance of illegal driving, it’s not directly clear, and there’s no evidence provided. Therefore, this is a weak argument.
B. This statement is irrelevant as it’s making its own argument, providing a different outcome of a reduced driving age. There is also no evidence provided to suggest that the number of young people smoking cannabis on the street wil be reduced simply by reducing the driving age. Therefore, this is also a weak argument.
C. This is another subjective statement and it doesn’t address the issue of illegal driving. It addresses a separate issue which is unrelated to the subject matter. Therefore, it is a weak argument.
D. This statement directly addresses the subject matter, providing a factual basis, therefore it’s a strong argument. Because there is no association between age and likelihood of legal driving, there is no need to reduce the legal driving age in an attempt to decrease illegal driving.
UCAT Online Course – by the top 1%
Our UCAT online course consists of 154 bite-sized videos covering everything you need to know about the UCAT. You get access for the whole season, until the last day of UCAT! Learn practical methods of improving your speed, strategies and score, with content created by the top 1% scoring candidates.
UCAT Decision Making Venn Diagrams
A Venn diagram is used to represent relationships between different elements, with overlaps suggesting a common factor, and the non-overlapping areas suggesting something unique to the set in question. Venn diagrams can come in different shapes, sizes, and combinations.
Example:
The diagram below depicts the result of a survey conducted on USA citizens that travelled to Italy, France and Greece in the last year. Tourists from USA require a visa to enter any country in the west of Europe. Greece belongs to the east of Europe and the other countries in the survey belong to the west. Those who visited France spent a minimum of $3500, whereas those who visited Italy spent a maximum of $5000, and those who visited Greece spent a minimum of $2500 on souvenirs. Obtaining a visa costs an additional fee of $300.
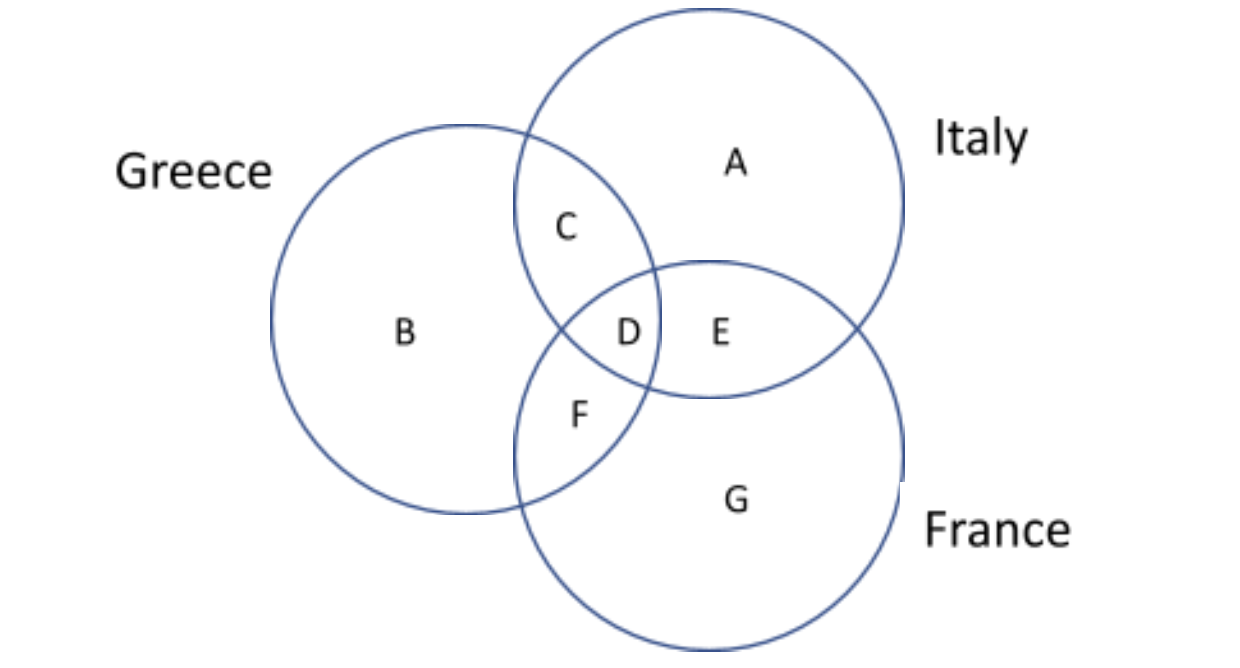
Which of the following statements is true about the tourists?
- A. Those belonging to category D spent a maximum of $6000.
- B. Those who belong to category G required a visa and spent a maximum of $7000.
- C. Those who belong to category D spent a minimum of $300 more than those who belong to category F.
- D. Those who belong to category C spent a maximum of $7800
Strategy:
Simplify the data before reading the questions, as they will be much easier to understand once you understand the data. This can be done as follows:

Note: On your whiteboard or scratchpad, this can be simplified much further. Try using initials to represent countries, “Y” and “N” or a check and cross rather than “Yes” or “No”, and omitting the column headers. After interpreting the data, eliminate options by focusing on the ones that are most easily calculable.
There are seven Venn diagrams that we have named the “Seven HeaVenns”. Going through these Seven HeaVenns, you will learn to appreciate how Venn diagrams can be used to clarify the relationships between different objects in a syllogism. To learn more about the 7 HeaVenss, including image examples, check out our free resource on UCAT Syllogisms.
UCAT Decision Making Logical Puzzles Example
Logical puzzle scenarios in UCAT Decision Making involve a large number of details which you must interpret in a format that’s reasonable for yourself to understand. They can be nearly impossible to solve without using a whiteboard to simplify the information. Logical puzzles may appear as a drag-and-drop format, but are generally in the form of option selection.
Example:
Daniel, Mohammed, Adrian, Aaron, Stephanie, and Rachel went shopping together and bought trousers. These trousers were either short, medium, or long in length and black, red, or grey in colour.
- Only one of the friends had medium length trousers
- Daniel’s trousers were long and were not black in colour
- There was one more pair of long trousers than short trousers
- Mohamed and Rachel bought the exact same trouser length and colour combination
- The length of Daniel’s trousers was exactly the same as Rachel’s
- The number of black trousers was equal to the number of long ones
- There was only one pair of red trousers and they belonged to Daniel
- Rachel’s trousers were grey in colour
Which of the following combinations of trouser length and colour is possible?
A. Adrian’s trousers were medium and black.
B. Rachel’s trousers were short and grey.
C. Aaron’s trousers were medium and grey.
D. Daniel’s trousers were short and red.
Strategy:
We can fill in a table using the information as follows:
| Name | Trouser Length | Trouser Colour |
| Daniel | Long | Red |
| Mohammed | Long | Grey |
| Adrian | Black | |
| Aaron | Black | |
| Stephanie | Black | |
| Rachel | Long | Grey |
It’s clear from the table that options B, C, and D cannot be true. Rachel’s trousers are long, Aaron’s are black, and Daniel’s are long. The question asks what is possible. Adrian’s trousers must be black, and they are either short or medium length. Thus, it’s possible that they are medium length.

Medicine & Dentistry Application Packages
Applying for 2025/26 entry? Get full support through A-Z of your application with a tailored application package. Includes UCAT, personal statement, interviews, A-levels, strategic applications, 24/7 live chat, and monthly progress meetings.
UCAT Decision Making Tips
Prepare for the Type of Data that Will be Presented to You
In the UCAT Decision Making section, you’ll encounter various types of data, such as graphs, charts, tables, and written information. To perform well, it’s essential to familiarize yourself with these formats during your preparation. Practice interpreting data quickly and accurately, and focus on identifying key trends, patterns, and relationships. The more you practice, the faster and more efficiently you’ll be able to analyze and make decisions based on the data presented to you during the exam.
Find the Answer Within Equations 1-3
After making some substitutions to equation 4, you’ll often find that you are left with a question mark on one side, which represents a single missing shape, and the other side looks exactly like one of the sides present in equations 1-3. You can use that equation to deduce the shape that’s represented by the question mark.
Find the Fastest Way To Solve an Equation
There are many ways to solve an equation. You need to find the fastest and most effective way to do so. During your Decision Making practice, if there’s a question that’s taken you many, many steps to solve, try it again. Find a faster way, as there will be one. This will help you quickly solve future questions that have a similar pattern of equations.
Know Which Equations Need To Be Discarded
Any equation with a shape that exists nowhere else in all of the equations should be discarded immediately. That equation is there to waste your time. You can rearrange and substitute as much as you like, but you’ll always have that single shape that you cannot make use of.
Don’t Add Extra Shapes Into Equation 4
Try not to substitute any shape into equation 4 that doesn’t already exist there. Sometimes, it will be necessary to do so, as you might need to completely replace one of the shapes in equation 4 with another one in order to solve the equation. However, unless you recognise an absolute need to add an extra shape, do not do this!
Understand what makes a Strong Argument
In the UCAT Decision Making section, a strong argument is logical, relevant, and evidence-based. It should directly address the question, avoid emotional reasoning, and be supported by facts. To identify strong arguments, focus on spotting bias, assessing relevance, and recognizing assumptions. By practicing these skills, you can effectively evaluate arguments and improve your UCAT Decision Making score.
Only Use the Knowledge Presented to You
It’s important to ensure no bias is present in your thought process when evaluating an argument. The questions will commonly contain themes that are of general knowledge, so many students may have their own opinions on them. Furthermore, when a question is worded as “Should X occur?”, it’s easy to use your own biases when deciding the correct answer. However, you must ensure that you only use the knowledge presented to you and evaluate the argument based on facts and relevance to the subject matter.
Eliminate and Estimate
If you’re running out of time, you can guess an answer after eliminating some options, as your chances of guessing the correct answer increase after each elimination. You may find it quicker to draw your own Venn diagram, but generally, this can take much longer as you need to continually account for each of the values added in each overlap of a circle, subtracting it from the total. Also, you don’t need to go in order of the paragraph, but rather you can choose any sentence and eliminate in a way that works for you. However, if you have a routine of following the order of the paragraph, this may save you time as your brain is accustomed to answering the question in a specific way.
Use Keyboard Shortcuts in UCAT Decision Making
Mastering keyboard shortcuts can save valuable time in this section. Instead of relying on the mouse, use shortcuts to navigate questions quickly, eliminate answers, and move between sections. This improves efficiency, reduces time pressure, and allows for faster decision-making. Practicing with shortcuts during preparation will help you maximize speed and accuracy on test day.
Answer Every Question
Since the UCAT has no negative marking, it’s crucial to attempt every question, even if you’re unsure. Leaving a question blank guarantees zero marks, but making an educated guess gives you a chance to score points. Use strategies like eliminating wrong answers, recognizing patterns, and managing time effectively to improve accuracy. Even a guessed answer has a chance of being correct, so always select an option before moving on.
Practice and Get UCAT Tutoring
Consistent practice is key to succeeding in the UCAT, especially in the Decision Making section. Working through a variety of questions will help you become familiar with the question types and improve your reasoning skills. Additionally, if you’re finding certain areas challenging, UCAT tutoring can provide personalized guidance. A tutor can help you identify weaknesses, refine strategies, and boost your confidence. Combining self-study with expert support is an effective approach to mastering the UCAT.
We hope this article was useful for your UCAT preparation! It’s an excerpt from our popular UCAT book, created by top 1% scoring candidates!
UCAT Tutoring by Top 10% Scorers
Skyrocket your UCAT score with one-on-one mentoring with an expert UCAT tutor. We focus on your weakest areas and deliver personalised preparation to help you reach your highest potential.














